审核求过

这是在咕了一周的每日总结以及一次每周总结的情况下写的题解

其实蛮简单的....就是没有有图的题解。

考虑每个$a_i$只能选一次的限制，这个太典了，直接拆点$in_i,out_i$，连一条容量 $1$ ,费用 $1$ 的边，走了这条边意味着选了 $a_i$ , 并且产生 $1$ 的贡献。

然后思考两个限制，相邻元素绝对值差为 $1$ ,或模 $7$ 同余。

显然有这么一种思路，从 $out_i$ 向之后所有的与它差为 $1$ 或模 $7$ 同余的点的 $in_i$ 连边，但这样边数是 $O(n^2)$ 的，显然过不了。

考虑从 $a_i$ 到 $a_j$ ，如果中间有一个一样可以到达 $a_i$ ，$a_j$ 的点 $a_k$ , 那么从 $a_i$ 到 $a_k$ ，再从 $a_k$ 到 $a_j$ 是完全可以替代 $a_i,a_j$ 的。

因此继续拆点，将$a_i$再拆成$sub_i,mod_i$ ，用于与绝对值差为 $1$ ，以及膜 $7$ 同余的 最近点 连边。

具体连边像这样（容量、费用）

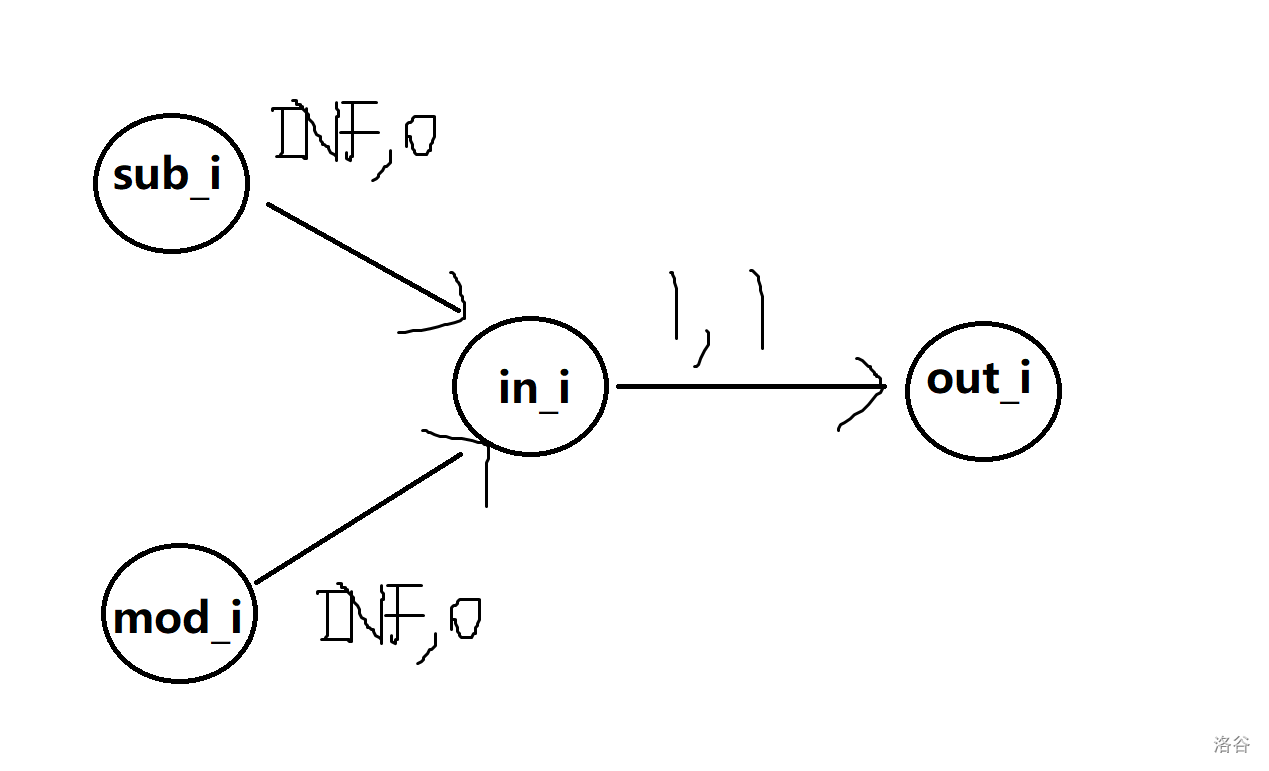
然后在相邻的模 $7$ 同余的点的 $mod_i$ 之间连 $(INF，0)$ 的边（不选），在相邻的 $a_i$ 相同的点的 $sub_i$ 之间连 $(INF，0)$ 的边（这些是表示不用选自己就可以选到自己后面的）。从每个点的 $out_i$ 向之后最近的 $a_i-a_j==1$ 的点和 $a_j-a_i==1$ 的点的 $sub_i$ 连 $(INF，0)$ 的边，向之后最近的模 $7$ 同余的节点的 $mod_i$ 连 $(INF，0)$ 的边。（表示选了自己后能选后面的）

然后从源点向每个点的 $in_i$ 连 $(INF，0)$ 的边，从每个点的 $out_i$ 向汇点连 $(INF，0)$。

最后有一个子序列数量的限制，我们建一个超级源点，向源点连容量为需要的子序列数，费用为 $0$ 的边。（所以其实 $k-Melodies$ 都是能做的）

附上样例二的建图

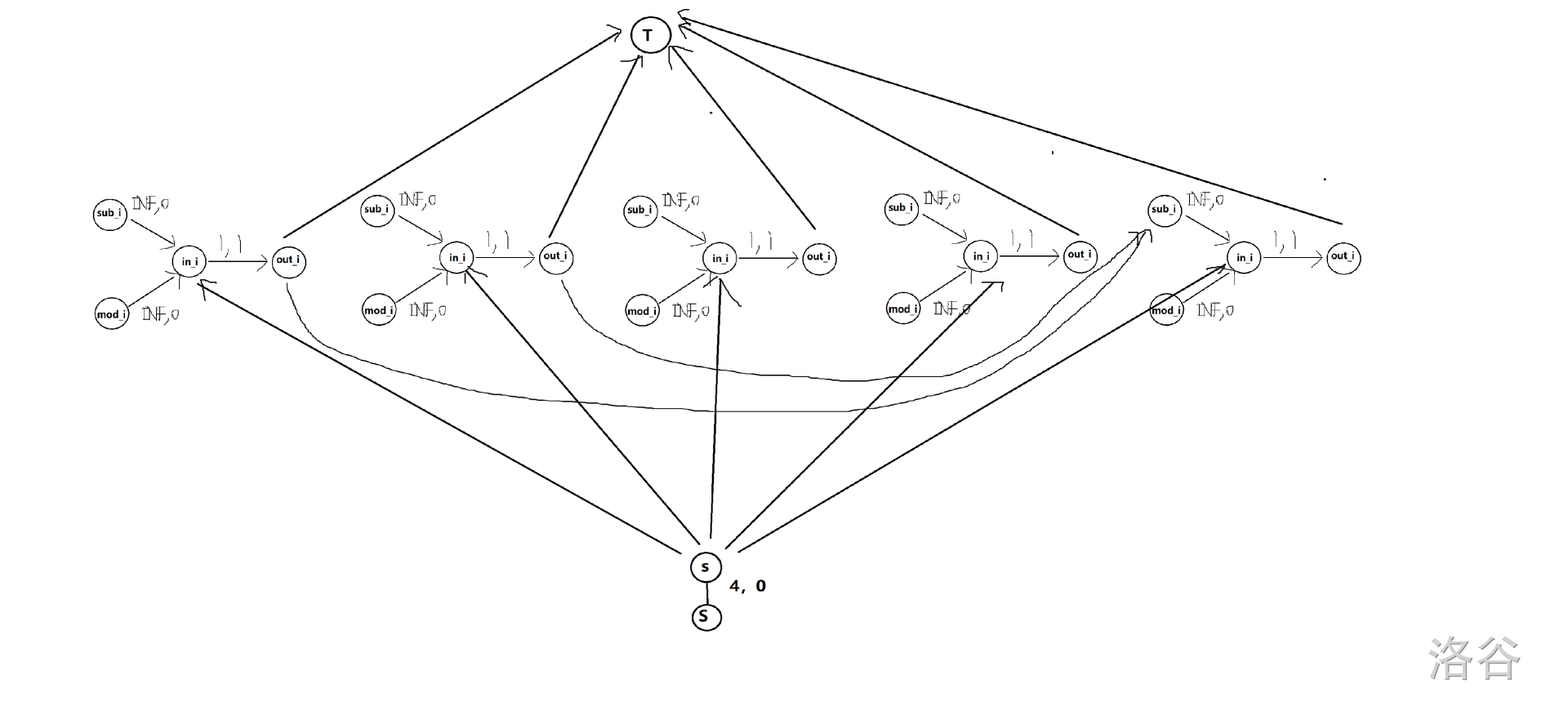
很丑陋吧?画图画的

附上代码

// Problem: CF818G Four Melodies
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF818G
// Memory Limit: 1000 MB
// Time Limit: 5000 ms
#include<bits/stdc++.h>
#define N 20010
#define M 1000010
using namespace std;
namespace MCMF{
	int cnt=1,head[N],to[M],nxt[M],val[M],flow[M];
	const int INF=0x3f3f3f3f;
	void insert(int u,int v,int f,int w){
		cnt++;
		to[cnt]=v;
		val[cnt]=w;
		flow[cnt]=f;
		nxt[cnt]=head[u];
		head[u]=cnt;
	}
	void ins(int u,int v,int f,int w) {
		insert(u,v,f,w);
		insert(v,u,0,-w);
	}
	int wat[N],dis[N],vis[N],fr[N];
	int SPFA(int ss,int tt) {
		memset(dis,-1,sizeof(dis));
		queue<int> q;
		q.push(ss),dis[ss]=0,wat[ss]=INF,vis[ss]=1;
		while(!q.empty()) {
		    int now=q.front();q.pop();
		    vis[now]=0;
		    for(int i=head[now]; i; i=nxt[i]) 
		        if(flow[i]&&dis[to[i]]<dis[now]+val[i]) {
		        	dis[to[i]]=dis[now]+val[i];
		        	fr[to[i]]=i;
		        	wat[to[i]]=min(wat[now],flow[i]);
		        	if(!vis[to[i]]) q.push(to[i]),vis[to[i]]=1;
		        }
		}
		return dis[tt]!=-1;
	}
	pair<int,int> Dinic(int ss,int tt) {
		int rf=0,rv=0;
		while(SPFA(ss,tt)) {
			rf+=wat[tt],rv+=wat[tt]*dis[tt];
			int now=tt;
			while(now!=ss) {
				flow[fr[now]]-=wat[tt];
				flow[fr[now]^1]+=wat[tt];
				now=to[fr[now]^1];
			}
		}
		return make_pair(rf,rv);
	}
}
using namespace MCMF;
int read() {
	int res=0,f=1;char ch=getchar();
	while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
	while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
	return f*res;
}
int S,s,T,n,num[N];
int main()
{
	n=read();s=4*n+1,T=4*n+2;
    for(int i=1; i<=n; i++) num[i]=read();
    ins(S,s,4,0);
    for(int i=1; i<=n; i++) {
    	ins(s,2*n+i,INF,0),ins(i,2*n+i,INF,0),ins(n+i,2*n+i,INF,0);
    	ins(2*n+i,3*n+i,1,1),ins(3*n+i,T,INF,0);
    	for(int j=i+1;j<=n;j++)if(num[i]-num[j]==1){ins(n*3+i,n+j,INF,0);break;}
		for(int j=i+1;j<=n;j++)if(num[j]-num[i]==1){ins(n*3+i,n+j,INF,0);break;}
		for(int j=i+1;j<=n;j++)if(num[i]%7==num[j]%7){ins(n*3+i,j,INF,0),ins(i,j,INF,0);break;}
		for(int j=i+1;j<=n;j++)if(num[i]==num[j]){ins(n+i,n+j,INF,0);break;}
    }
    cout<<Dinic(S,T).second;
    return 0;
}