难得自己想出来的黑题，祭之。

每一次修改会覆盖数个相同颜色的段，每个相同颜色的段提供一次贡献，我们考虑只在这个相同颜色段的深度最大处统计这个贡献。

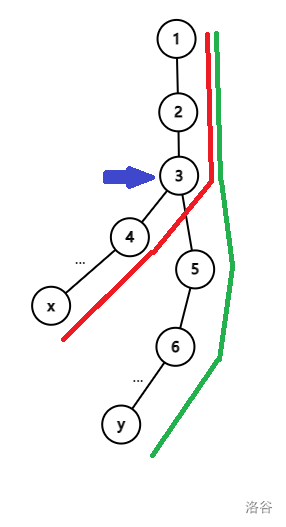
如该图所示，当红绿两次修改操作发生时，将在点 $3$ 处统计一次贡献。

对每个点考虑它的贡献。当且仅当 它的子树中发生两次修改操作，且这两次修改操作属于不同颜色，操作位置属于不同儿子时 它会提供一次贡献（这里注意这个节点本身也可以被算入贡献）。

我们设当前的点为 $now$ ，将 $now$ 的每个儿子的子树的次数和设为一类，将自己的次数设为一类。所求的这个节点的最大修改数，即为将这些类内的元素交错摆放，使得相邻两个元素所属的类不同的情况出现的次数最多。

这个讨论本质上是 CF1649B ，这里不再过多赘述。设所有类的大小之和为 $sum$ ，其中大小最大的类的大小为 $max$ ，则该点所能产生的最大贡献为 $min(sum-1,2 \times (sum-max))$ 。

发现一个点按自己产生最大贡献的标准排列子树内的操作，也只是排列其 相对位置 ，祖先节点可以任意地在中间插入操作。因此每个节点的贡献之间是 不相关 的。于是我们可以用树形 dp 解决，这里就能拿到不带修改的 $30pt$ 。

考虑修改。修改本质上是一个链加。我们将节点的贡献分为三种：由 $sum-1$ 贡献来的，由自己作为 $max$ 贡献来的，由自己的一个儿子作为 $max$ 贡献来的。考虑如果是第三种情况，即用自己儿子贡献来的，我们将这个节点与贡献的儿子连在一起，这样会形成一些 重链 。考虑一个修改，如果是对于一个重链一起修改，那么由于 $sum$ 和 $max$ 都会加上 $w$ ，因此重链内部的贡献不变。变的只有重链之间轻边的贡献，因此用一个 LCT 维护轻边贡献并实时更改重链即可，时间复杂度 $O(nlogn)$ 。

$Code$

#include<bits/stdc++.h>
#define int long long
#define N 800010
using namespace std;
int cnt,head[N],to[N<<1],nxt[N<<1];
void insert(int u,int v){ 
    cnt++;
    to[cnt]=v;a
    nxt[cnt]=head[u];
    head[u]=cnt;
}
int siz[N],son[N],ans,mx[N],a[ASN],oth[N],type[N];
namespace LinkCutTree{
	int c[N][2],laz[N],f[N];ASD
	bool ntrt(int x) {return cA[f[x]][0]==x||c[f[x]][1]==x;}
	void pushup(int x) {
		siz[x]=siz[c[x][0]]+siz[c[x][1]]+oth[x]+a[x];
	}
	void rotate(int x) {
		int y=f[x],z=f[y],k=c[y][1]==x,w=c[x][!k];
		if(ntrt(y)) c[z][c[z][1]==y]=x;
		c[x][!k]=y,c[y][k]=w;
		if(w) f[w]=y;
		f[y]=x,f[x]=z;
		pushup(y),pushup(x);
	}
	void splay(int x) {
		while(ntrt(x)) {
			int y=f[x],z=f[y];
			if(ntrt(y)) rotate((c[z][0]==y)^(c[y][0]==x)?x:y);
			rotate(x);
		}

	}
	void access(int x,int z) {
		for(int vid=0; x; x=f[vid=x]) {
			splay(x);
			int tot=siz[x]-siz[c[x][0]];
			if(type[x]==0||type[x]==1) {
				ans-=2*(tot-(type[x]?a[x]:siz[c[x][1]]));
			} else ans-=tot-1;
			tot+=z;siz[x]+=z;
			if(vid) oth[x]+=z;
			else a[x]+=z;
			if(2*siz[vid]>=tot+1) oth[x]+=siz[c[x][1]]-siz[vid],c[x][1]=vid;
			if(2*siz[c[x][1]]>=tot+1) type[x]=0,ans+=(tot-siz[c[x][1]])<<1;
			else {
				if(c[x][1]) oth[x]+=siz[c[x][1]],c[x][1]=0;
				if(2*a[x]>=tot+1) type[x]=1,ans+=(tot-a[x])*2;
				else type[x]=2,ans+=tot-1;
			}
		}
	}

}
using namespace LinkCutTree;
inline void dfs(int now,int fa){
	f[now]=fa,siz[now]=a[now],son[now]=0,mx[now]=a[now];
	for(int i=head[now]; i; i=nxt[i]) if(to[i]!=fa) {
		dfs(to[i],now);
		mx[now]=max(mx[now],siz[to[i]]);
		if(siz[to[i]]>siz[son[now]]) son[now]=to[i];
		siz[now]+=siz[to[i]];
	}
	oth[now]=siz[now]-a[now];
	ans+=min(siz[now]-1,siz[now]-(mx[now]-(siz[now]-mx[now])));
	if(2*siz[son[now]]>=siz[now]+1) { type[now]=0,c[now][1]=son[now],oth[now]-=siz[son[now]];return ;}
	if(2*a[now]>=siz[now]+1) {type[now]=1;return ;}
	type[now]=2;
} 
int n,m;
signed main()
{
//	freopen("history.in","r",stdin);
//	freopen("history.out","w",stdout);
	scanf("%lld%lld",&n,&m);
//	siz[0]=-1;
	for(int i=1; i<=n; i++) scanf("%lld",&a[i]);
//	cout<<"End\n";
	for(int i=1; i<n; i++) {
		int u,v;
		scanf("%lld%lld",&u,&v);
		insert(u,v);
		insert(v,u);
	}
//	printf("End\n");
	dfs(1,0);
//	for(int i=1; i<=n; i++) printf("%lld ",type[i]);
//	puts("");
//	printf("END\n");
	printf("%lld\n",ans);
    while(m--) {
    	int x,z;
    	scanf("%lld%lld",&x,&z);
    	access(x,z);
    	printf("%lld\n",ans);
	}
}