

【学习笔记】线段树分治
热度: loading...
什么是线段树分治啊(战术后仰)
考虑这样一个问题,这个问题包含:
-
个操作,每个操作覆盖一段时间区间。
-
次询问,每次询问某个时间的答案。
很显然,如果我们要获取一个时间的答案就需要统计覆盖这个时间的所有操作的贡献。
一种很常见的想法就是在线处理,在每个操作出现时计算贡献,在每个操作消失时删除贡献。
但是在很多问题中,在线算法不便于维护信息甚至根本无法维护信息,这时我们就需要线段树分治 。
简而言之,线段树分治的根本思想是在时间轴上建立一棵线段树,将每个操作挂到它所覆盖的时间区间所对应的线段树节点上。
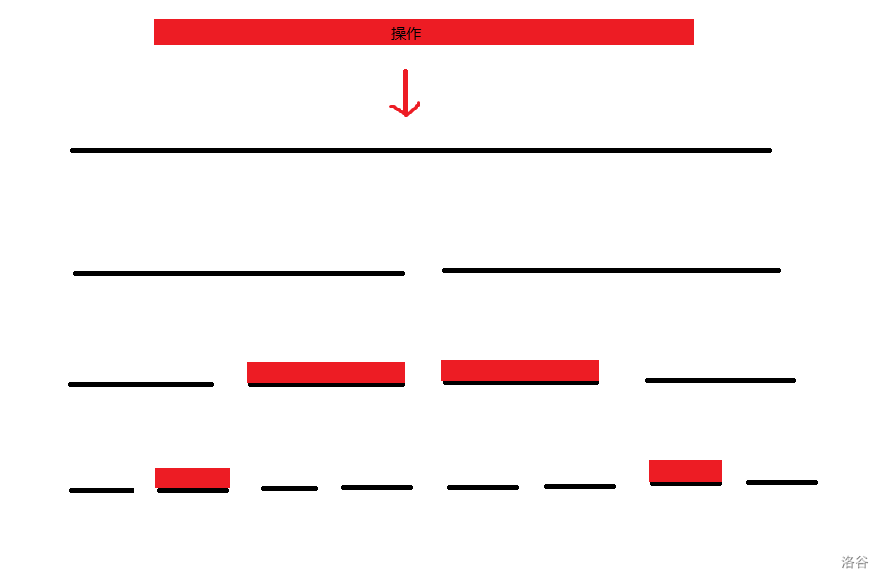
注意并不需要下传
之后我们直接对于整个时间区间分治,遍历线段树的每个节点。进入每个节点时处理挂在这个节点上的所有修改操作并统计贡献。可以证明,在我们遍历到一个单独的时间点时,覆盖在这个时间点上的所有操作一定都处理完了,于是直接输出答案即可。
在退出一个节点是,将这个节点上的所有修改操作全部撤回,回退贡献。
适合搭配一些支持撤回最新操作,不方便直接消除之前操作贡献的数据结构使用。
时间复杂度分析:每个操作最多会被挂到 个节点上,设每个操作的复杂度是 ,总的时间复杂度为 。
例题
使用可撤销扩展域并查集维护二分图贡献。将一个点 拆分为两个点 ,连边 时将 , 所在的集合合并。若存在任意一个节点 使得 属于同一集合,则不属于二分图。进入一个节点时将挂在该节点上的所有边加入并查集,维护贡献,并在退出节点是将并查集回退到进入之前的状态即可。
// Problem: P5787 二分图 /【模板】线段树分治
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P5787
// Memory Limit: 256 MB
// Time Limit: 1000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
#define N 200010
#define mid (l+r)/2
#define ls k*2
#define rs k*2+1
#define pb push_back
using namespace std;
int read() {
int res=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
return f*res;
}
int n,m,K,fa[N],siz[N];
struct Edge{
int x,y;
}e[N];
struct node{
int x,y,siz;
}sk[N];
int find(int x) {
while(fa[x]!=x) x=fa[x]=fa[fa[x]];
return x;
}
int top;
void merge(int x,int y) {
int fx=find(x),fy=find(y);
if(siz[fx]>siz[fy]) swap(fx,fy);
sk[++top]=node{fx,fy,siz[fy]};
fa[fx]=fy,siz[fy]+=siz[fx];
}
vector<int> p[N<<2];
void update(int k,int l,int r,int L,int R,int id) {
if(L<=l&&r<=R) {p[k].pb(id);return ;}
if(L<=mid) update(ls,l,mid,L,R,id);
if(R>mid) update(rs,mid+1,r,L,R,id);
}
void solve(int k,int l,int r) {
int ans=1,las=top;
for(int i=0; i<p[k].size(); i++) {
int fx=find(e[p[k][i]].x);
int fy=find(e[p[k][i]].y);
if(fx==fy) {
for(int j=l; j<=r; j++) printf("No\n");
ans=0;break;
}
merge(e[p[k][i]].x,e[p[k][i]].y+n);
merge(e[p[k][i]].x+n,e[p[k][i]].y);
}
if(ans) {
if(l==r) printf("Yes\n");
else solve(ls,l,mid),solve(rs,mid+1,r);
}
while(top>las) {
siz[sk[top].x]=siz[sk[top].y]-sk[top].siz;
siz[sk[top].y]=sk[top].siz;
fa[sk[top].x]=sk[top].x;
top--;
}
}
int main()
{
n=read(),m=read(),K=read();
for(int i=1; i<=2*n; i++) fa[i]=i,siz[i]=1;
for(int i=1; i<=m; i++) {
e[i]=Edge{read(),read()};
int l=read()+1,r=read();
update(1,1,K,l,r,i);
}
solve(1,1,K);
return 0;
}
CF1140F Extending Set of Points
将点 视作在第 行和第 列中连边,很显然这是一个二分图。同样用并查集维护,贡献即为每个连通块中两侧节点数的乘积之和。
// Problem: CF1140F Extending Set of Points
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/CF1140F
// Memory Limit: 1000 MB
// Time Limit: 3500 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
#define ls k*2
#define rs k*2+1
#define mid (l+r)/2
#define mp make_pair
#define fi first
#define se second
#define pb push_back
#define int long long
#define N 600010
using namespace std;
typedef pair<int,int> pii;
int read() {
int res=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
return f*res;
}
int n,fa[N],size[N],tp;
pii siz[N];
int find(int x) {
while(fa[x]!=x) x=fa[x];
return x;
}
map<pii,int> pt;
vector<pii> p[N<<2];
int res;
struct node{
int x,y;
pii siz;
int size,res;
}sk[N];
void merge(int x,int y) {
x=find(x),y=find(y);
if(x==y) return ;
if(size[x]>size[y]) swap(x,y);
sk[++tp]=node{x,y,siz[y],size[y],res};
res-=1ll*siz[x].fi*siz[x].se+1ll*siz[y].fi*siz[y].se;
fa[x]=y,size[y]+=size[x];
siz[y]=mp(siz[y].fi+siz[x].fi,siz[y].se+siz[x].se);
res+=1ll*siz[y].fi*siz[y].se;
}
void modify(int k,int l,int r,int L,int R,pii val)
{
if(L<=l&&r<=R) {p[k].pb(val);return ;}
if(L<=mid) modify(ls,l,mid,L,R,val);
if(R>mid) modify(rs,mid+1,r,L,R,val);
}
void solve(int k,int l,int r) {
int las=tp;
for(int i=0; i<p[k].size(); i++)
merge(p[k][i].fi,p[k][i].se);
if(l==r) printf("%lld ",res);
else solve(ls,l,mid),solve(rs,mid+1,r);
while(tp>las) {
int x=sk[tp].x,y=sk[tp].y;
fa[x]=x,size[y]=sk[tp].size;
siz[y]=sk[tp].siz;
res=sk[tp].res;
tp--;
}
}
signed main()
{
n=read();
for(int i=1; i<=n; i++) {
pii tmp=mp(read(),read()+300000);
if(pt[tmp]) modify(1,1,n,pt[tmp],i-1,tmp),pt.erase(tmp);
else pt[tmp]=i;
}
for(int i=1; i<=600000; i++)
fa[i]=i,siz[i]=((i<=300000)?mp(1,0):mp(0,1)),size[i]=1;
for(auto i:pt) modify(1,1,n,i.se,n,i.fi);
solve(1,1,n);
return 0;
}
同样的,对于每个修改操作离线挂到线段树上,由于询问也有时间限制,因此将询问也挂到线段树上,对所有结果取最大即可。注意这里还有一维空间限制,构建可持久化 trie 树,处理修改时将其加入 trie 树,处理询问时统计 trie 树中 的贡献。
// Problem: P4585 [FJOI2015]火星商店问题
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P4585
// Memory Limit: 500 MB
// Time Limit: 2000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
#define N 200010
#define mid (l+r)/2
using namespace std;
int n,m,rt[N],tr[N*20][2],tot,tim[N*20];
int ans[N];
struct query{int l,r,L,R,x;}p[N];
struct ist{int s,v,t;}q[N],sk1[N],sk2[N];
const bool cmp(ist x,ist y){return x.s<y.s;}
int cnt1,cnt2;
long long pos(long long x,long long pos){return ((x&(1<<pos))>0);}
int calc(int l,int r,int num) {
int res=0;
int ar=r,al=l;
for(int i=17; i>=0; i--) {
if(tim[tr[ar][!pos(num,i)]]>tim[tr[al][!pos(num,i)]]) {
ar=tr[ar][!pos(num,i)];
al=tr[al][!pos(num,i)];
res=res|(1ll<<i);
} else {
ar=tr[ar][pos(num,i)];
al=tr[al][pos(num,i)];
}
}
return res;
}
vector<int> a[N];
void update(int rt,int l,int r,int L,int R,int x) {
if(L>R||r<L||l>R) return ;
if(L<=l&&r<=R) {a[rt].push_back(x); return ;}
update(rt*2,l,mid,L,R,x); update(rt*2+1,mid+1,r,L,R,x);
}
int insert(int pre,int num) {
int RT=++tot,al=tot;
for(int i=17; i>=0; i--) {
tr[al][0]=tr[pre][0];
tr[al][1]=tr[pre][1];
tim[al]=tim[pre]+1;
tr[al][pos(num,i)]=++tot;
pre=tr[pre][pos(num,i)];
al=tr[al][pos(num,i)];
}
tim[al]=tim[pre]+1;
return RT;
}
int sk[N],top;
void dlwt(int x,int L,int R) {
top=tot=0;
for(int i=L; i<=R; i++) {
sk[++top]=q[i].s;
rt[top]=insert(rt[top-1],q[i].v);
}
for(int i=0,sz=a[x].size(); i<sz; i++) {
int k=a[x][i];
int l=upper_bound(sk+1,sk+1+top,p[k].l-1)-sk-1;
int r=upper_bound(sk+1,sk+1+top,p[k].r)-sk-1;
ans[k]=max(ans[k],calc(rt[l],rt[r],p[k].x));
}
}
void divide(int rt,int l,int r,int L,int R) {
if(L>R) return ;
int t1=0,t2=0;
dlwt(rt,L,R);
if(l==r) return ;
for(int i=L; i<=R; i++)
if(q[i].t<=mid) sk1[++t1]=q[i];
else sk2[++t2]=q[i];
for(int i=1; i<=t1; i++) q[i+L-1]=sk1[i];
for(int i=1; i<=t2; i++) q[i+L-1+t1]=sk2[i];
divide(rt*2,l,mid,L,L+t1-1);
divide(rt*2+1,mid+1,r,L+t1,R);
}
int read() {
int res=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
return f*res;
}
int main()
{
n=read(),m=read();
for(int i=1; i<=n; i++) rt[i]=insert(rt[i-1],read());
for(int i=1; i<=m; i++) {
int opt=read(),l,r,s,v,x,d;
if(!opt) s=read(),v=read(),q[++cnt1]=(ist){s,v,cnt1};
else {
l=read(),r=read(),x=read(),d=read();
ans[++cnt2]=calc(rt[l-1],rt[r],x);
p[cnt2]=(query){l,r,max(1,cnt1-d+1),cnt1,x};
}
}
for(int i=1; i<=cnt2; i++) update(1,1,cnt1,p[i].L,p[i].R,i);
sort(q+1,q+cnt1+1,cmp);
divide(1,1,cnt1,1,cnt1);
for(int i=1; i<=cnt2; i++) printf("%d\n",ans[i]);
return 0;
}
将所有加入边的操作离线到线段树上。维护一棵 LCT,加入边时判断两点是否连通,如果不连通则直接加入,连通则判断原路径上最大值是否大于当前值。如果是,则将最大值边断开,连上这条边。如此维护最小生成树即可。由于使用 LCT,记得将边权转换为点权。
// Problem: P3206 [HNOI2010]城市建设
// Contest: Luogu
// URL: https://www.luogu.com.cn/problem/P3206
// Memory Limit: 125 MB
// Time Limit: 3000 ms
//
// Powered by CP Editor (https://cpeditor.org)
#include<bits/stdc++.h>
#define mid (l+r)/2
#define ls k*2
#define rs k*2+1
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define int long long
using namespace std;
#define N 200010
typedef pair<int,int> pii;
int read() {
int res=0,f=1;char ch=getchar();
while(!isdigit(ch)) f=ch=='-'?-1:1,ch=getchar();
while(isdigit(ch)) res=res*10+ch-'0',ch=getchar();
return f*res;
}
int w[N];
namespace LinkCutTree{
int mx[N],c[N][2],laz[N],f[N];
bool ntrt(int x) {return c[f[x]][0]==x||c[f[x]][1]==x;}
void pushup(int x) {
mx[x]=x;
if(c[x][0]&&w[mx[c[x][0]]]>w[mx[x]]) mx[x]=mx[c[x][0]];
if(c[x][1]&&w[mx[c[x][1]]]>w[mx[x]]) mx[x]=mx[c[x][1]];
}
void rev(int x) {
swap(c[x][0],c[x][1]);
laz[x]^=1;
}
void pushdown(int x) {
if(laz[x]) {
if(c[x][0]) rev(c[x][0]);
if(c[x][1]) rev(c[x][1]);
laz[x]=0;
}
}
void rotate(int x) {
int y=f[x],z=f[y],k=c[y][1]==x,w=c[x][!k];
if(ntrt(y)) c[z][c[z][1]==y]=x;
c[x][!k]=y,c[y][k]=w;
if(w) f[w]=y;
f[y]=x,f[x]=z;
pushup(y);
}
int skt[N];
void splay(int x) {
int tmp=x;
int tott=0;
skt[++tott]=tmp;
while(ntrt(tmp)) skt[++tott]=tmp=f[tmp];
while(tott) pushdown(skt[tott--]);
while(ntrt(x)) {
int y=f[x],z=f[y];
if(ntrt(y)) rotate((c[y][0]==x)^(c[z][0]==y)?x:y);
rotate(x);
}
pushup(x);
}
void access(int x) {
for(int y=0; x; x=f[y=x])
splay(x),c[x][1]=y,pushup(x);
}
void makeroot(int x) {
access(x),splay(x),rev(x);
}
int findroot(int x) {
access(x),splay(x);
while(c[x][0]) pushdown(x),x=c[x][0];
splay(x);
return x;
}
void split(int x,int y) {
makeroot(x);
access(y),splay(y);
}
void link(int x,int y) {
makeroot(x);
if(findroot(y)!=x) f[x]=y;
}
void cut(int x,int y) {
makeroot(x);
if(findroot(y)==x&&f[y]==x&&!c[y][0]) {
f[y]=c[x][1]=0;
pushup(x);
}
}
}
using namespace LinkCutTree;
int n,m,q;
struct edge{
int u,v,w;
}e[N];
int tot,qr[N],las[N];
vector<int> p[N<<2];
void insert(int k,int l,int r,int L,int R,int id) {
if(L<=l&&r<=R) {p[k].pb(id);return ;}
if(L<=mid) insert(ls,l,mid,L,R,id);
if(R>mid) insert(rs,mid+1,r,L,R,id);
}
pii sk[N];
int tp,ans;
void solve(int k,int l,int r) {
int last=tp;
for(int i=0; i<p[k].size(); i++) {
int id=p[k][i],x=e[id].u,y=e[id].v,w=e[id].w;
if(findroot(x)==findroot(y)) {
split(x,y);int d=mx[y]-n;
if(e[d].w<=w) continue;
cut(e[d].u,d+n),cut(d+n,e[d].v);
sk[++tp]=mp(d,-1),ans-=e[d].w;
}
link(x,id+n),link(id+n,y);
sk[++tp]=mp(id,1),ans+=e[id].w;
}
if(l==r) printf("%lld\n",ans+1);
else solve(ls,l,mid),solve(rs,mid+1,r);
while(tp>last) {
int d=sk[tp].fi,x=e[d].u,y=e[d].v,w=e[d].w;
if(sk[tp].se==-1) link(x,d+n),link(d+n,y),ans+=w;
else cut(x,d+n),cut(d+n,y),ans-=w;
tp--;
}
}
signed main()
{
n=read(),m=n-1;
for(int i=1; i<=m; i++) {
e[++tot]=edge{read(),read(),read()},
w[n+tot]=e[tot].w;
insert(1,1,32766,1,32766,tot);
}
q=read();
for(int i=1; i<=q; i++) {
e[++tot]=edge{read(),read(),read()};
w[n+tot]=e[tot].w;
int l=read(),r=read();
insert(1,1,32766,l,r,tot);
}
solve(1,1,32766);
return 0;
}












